1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
|
# Fun with compute shaders and fluid dynamics
## First for some theory…
What we want (Navier-Stokes):
$$\begin{aligned} \partial_t \rho + \nabla \cdot (\rho u) &= 0 \\ \partial_t u + (u \cdot \nabla) u &= -\frac{1}{\rho} \nabla p + 2\nu\nabla \cdot (\mathrm{S})\end{aligned}$$
Pressure $p = c_s^2 \rho$
Kinetic viscosity: $\nu = c_s^2 \tau$
Tensor: $\mathrm{S} = \frac{1}{2} (\nabla u + (\nabla u)^\top)$
What we use (Boltzmann equilibrium):
$$\left( \partial_t + \xi \cdot \partial_x + \frac{F}{\rho} \cdot \partial_\xi \right) f = \Omega(f) \left( = \partial_x f \cdot \frac{dx}{dt} + \partial_\xi f \cdot \frac{d\xi}{dt} + \partial_t f \right)$$
How we get there (BGK LBM):
$$\Omega(f) := -\frac{f-f^\text{eq}}{\tau} \Delta t$$
$$(\partial_t + \xi \cdot \nabla_x) f = -\frac{1}{\tau} (f(x,\xi,t) - f^\text{eq}(x,\xi,t))$$
$$\newcommand{\V}[2]{\begin{pmatrix}#1\\#2\end{pmatrix}} \{\xi_i\}_{i=0}^8 = \left\{ \V{0}{0}, \V{-1}{\phantom{-}1}, \V{-1}{\phantom{-}0}, \V{-1}{-1}, \V{\phantom{-}0}{-1}, \V{\phantom{-}1}{-1}, \V{1}{0}, \V{1}{1}, \V{0}{1} \right\}$$
$$(\partial_t + \xi_i \cdot \nabla_x) f_i(x,t) = -\frac{1}{\tau} (f_i(x,t) - f_i^\text{eq}(x,t))$$
$$f_i^\text{eq} = w_i \rho \left( 1 + \frac{u \cdot \xi_i}{c_s^2} + \frac{(u \cdot \xi_i)^2}{2c_s^4} - \frac{u \cdot u}{2c_s^2} \right)$$
$$\rho(x,t) = \sum_{i=0}^{q-1} f_i(x,t)$$
$$\rho u(x,t) = \sum_{i=0}^{q-1} \xi_i f_i(x,t)$$
$$w_0 = \frac{4}{9}, \ w_{2,4,6,8} = \frac{1}{9}, \ w_{1,3,5,7} = \frac{1}{36}$$
$$\overline{f_i} = f_i + \frac{1}{2\tau}(f_i - f_i^\text{eq})$$
$$\overline\tau = \tau + \frac{1}{2}$$
$$\overline{f_i}(x+\xi_i,t+1) = \overline{f_i}(x,t) - \frac{1}{\overline\tau} (\overline{f_i}(x,t) - f_i^\text{eq}(x,t))$$
$$f_i^\text{out}(x,t) = f_i(x,t) - \frac{1}{\tau}(f_i(x,t) - f_i^\text{eq}(x,t))$$
$$f_i(x+\xi_i,t+1) = f_i^\text{out}(x,t)$$
## …translated into GLSL compute shaders
```cpp
layout (local_size_x = 1, local_size_y = 1) in;
layout (std430, binding=1) buffer bufferCollide{ float collideCells[]; };
layout (std430, binding=2) buffer bufferStream{ float streamCells[]; };
layout (std430, binding=3) buffer bufferFluid{ float fluidCells[]; };
uniform uint nX;
uniform uint nY;
```
```cpp
const uint q = 9;
const float weight[q] = float[](
1./36., 1./9., 1./36.,
1./9. , 4./9., 1./9. ,
1./36 , 1./9., 1./36.
);
```
```cpp
uint indexOfDirection(int i, int j) {
return 3*(j+1) + (i+1);
}
uint indexOfLatticeCell(uint x, uint y) {
return q*nX*y + q*x;
}
/* [...] */
float get(uint x, uint y, int i, int j) {
return collideCells[indexOfLatticeCell(x,y) + indexOfDirection(i,j)];
}
```
```cpp
float equilibrium(float d, vec2 v, int i, int j) {
return w(i,j) * d * (1 + 3*comp(i,j,v) + 4.5*sq(comp(i,j,v)) - 1.5*sq(norm(v)));
}
```
```cpp
void main() {
const uint x = gl_GlobalInvocationID.x;
const uint y = gl_GlobalInvocationID.y;
const float d = density(x,y);
const vec2 v = velocity(x,y,d);
setFluid(x,y,v,d);
for ( int i = -1; i <= 1; ++i ) {
for ( int j = -1; j <= 1; ++j ) {
set(x,y,i,j, get(x,y,i,j) + omega * (equilibrium(d,v,i,j) - get(x,y,i,j)));
}
}
}
```
```cpp
void main() {
const uint x = gl_GlobalInvocationID.x;
const uint y = gl_GlobalInvocationID.y;
if ( x != 0 && x != nX-1 && y != 0 && y != nY-1 ) {
for ( int i = -1; i <= 1; ++i ) {
for ( int j = -1; j <= 1; ++j ) {
set(x+i,y+j,i,j, get(x,y,i,j));
}
}
} else {
// rudimentary bounce back boundary handling
[...]
}
}
```
## Visuals
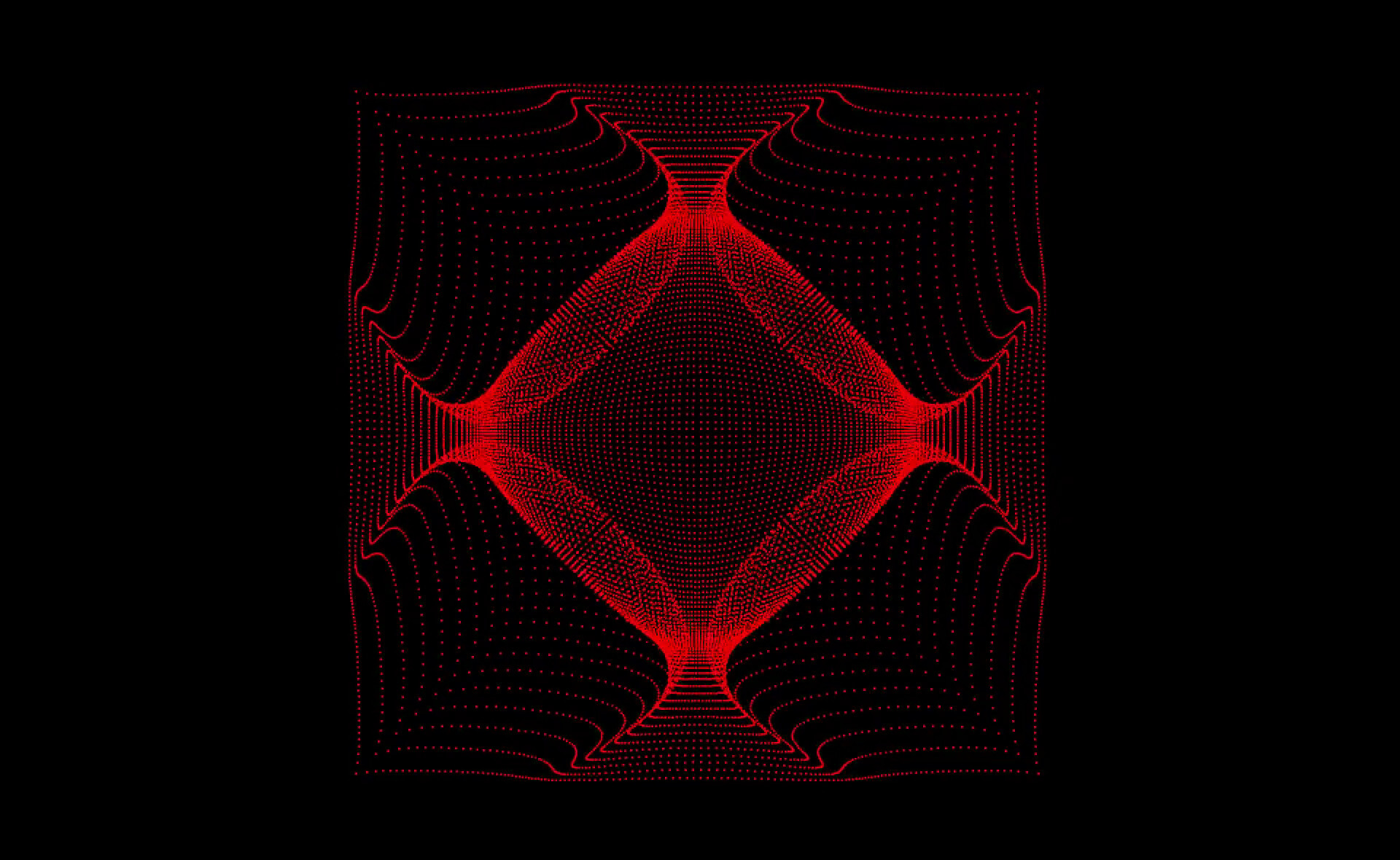
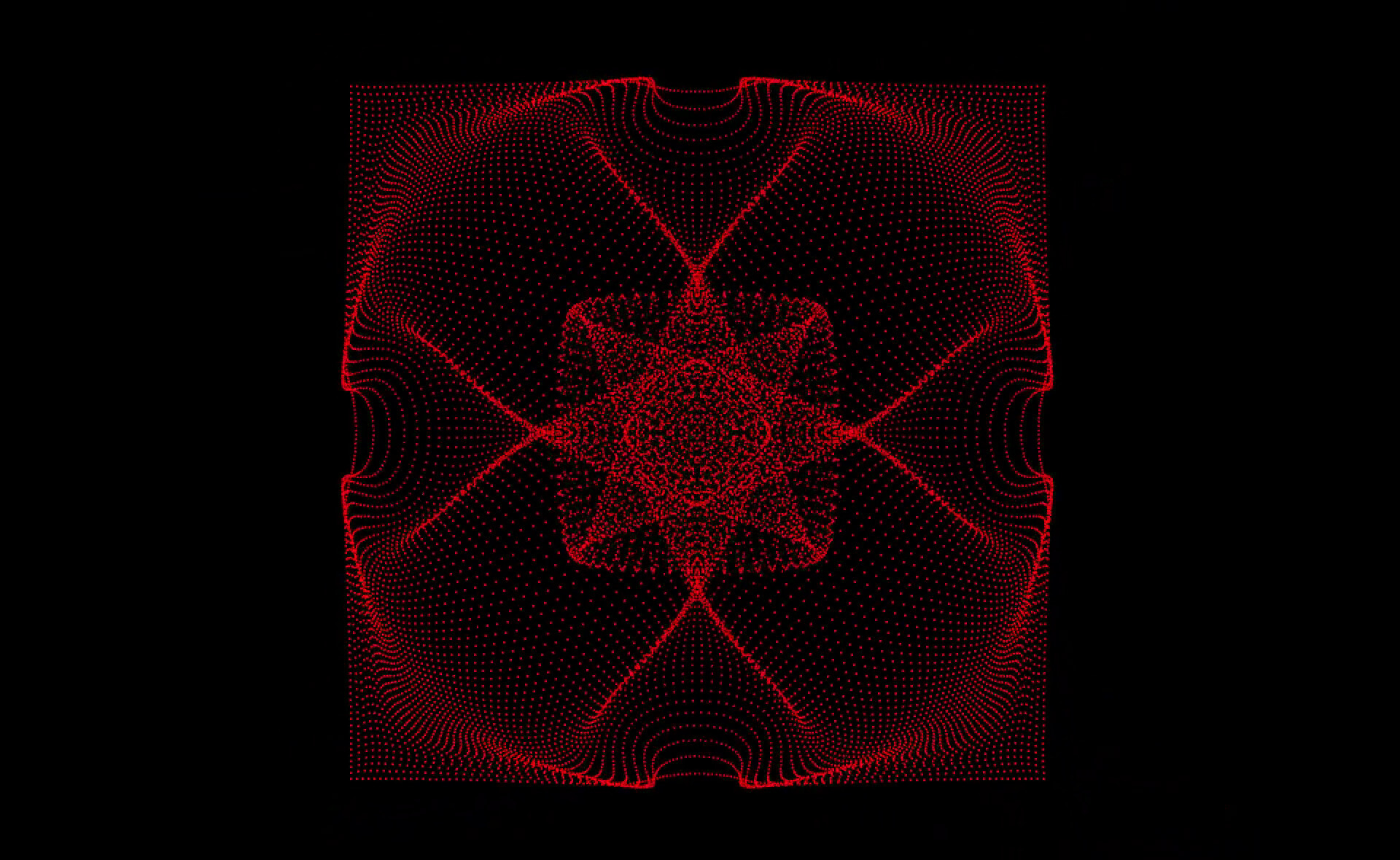

## Reaching down from the heavens
|
